The low quality of science, and why it matters
Ketil Malde
ketil.malde@imr.no
2015-03-19
Table of Contents
Introduction
Problem: Low reproducibility of scientific results
- Of 53 landmark cancer studies, six had reproducible results (Begley and Ellis, 2012)
- One third of top-cited research articles in medicine are later found to be exaggerated or wrong, 25% are never attempted reproduced (Ioannidis, 2005)
- 70% of experiments in psychology fail to be reproduced (http://www.psychfiledrawer.org/)
- Meta studies on TP53 and reboxetine (StatisticsDoneWrong)
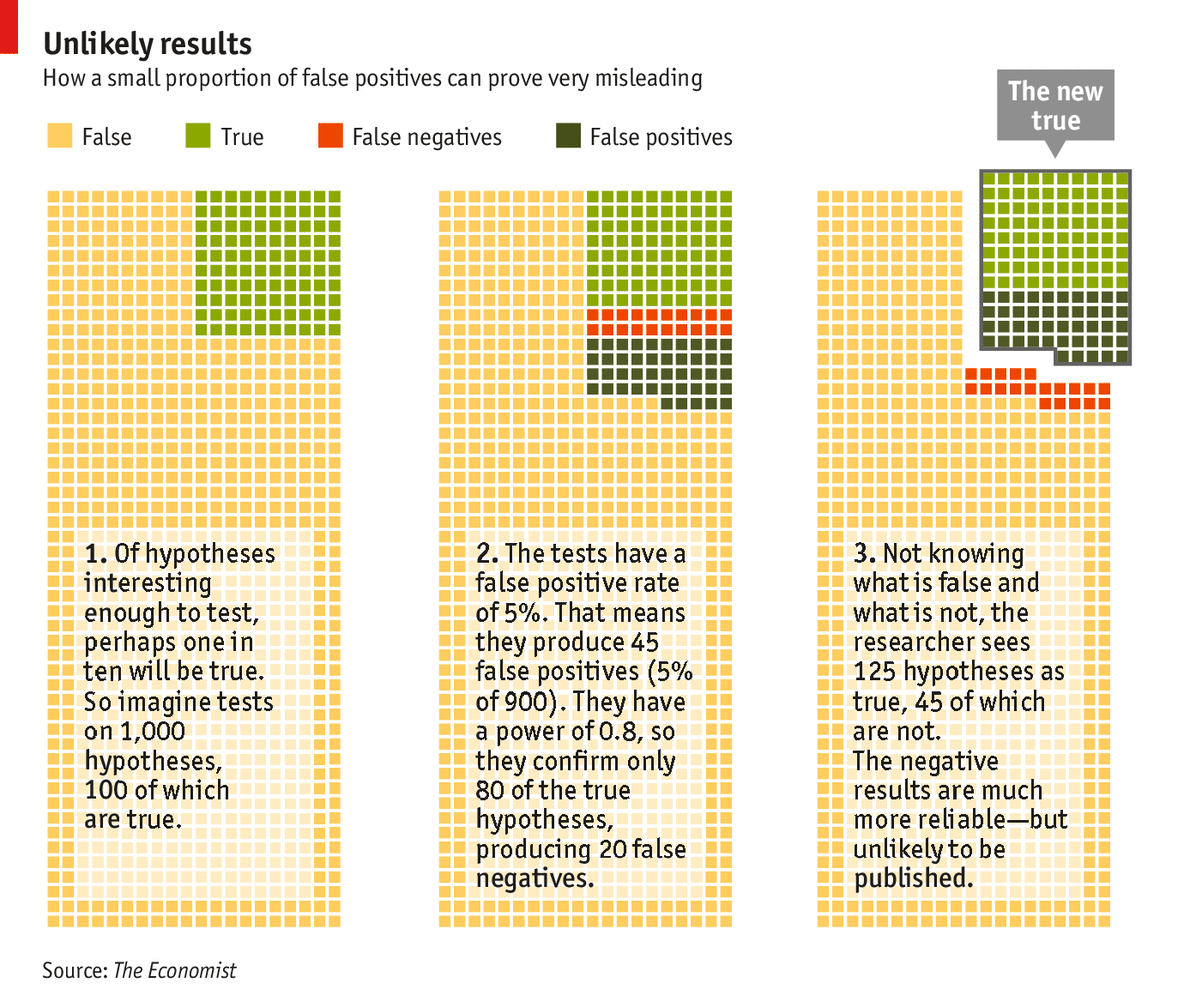
Why most published research findings are false

Breast cancer diagnosis
- 0.9% of patients have breast cancer
- test will correctly diagnose cancer in 90% of cases (power)
- 7% false positives
Excercise: Given a positive result from screening, what is the probability of having BC?
PPV - positive predictive value = posterior probability that a reported finding is true
The Basics
P-values and statistical power
- α: probability of rejecting a true null hypothesis (significance, i.e. p-value)
- β: probability of failing to reject a false hypothesis (power)
| True | False | |
|---|---|---|
| Accept | 1-β | α |
| Reject | β | 1-α |
| sum | 1 | 1 |
Note: PPV depends on α and β!
A priori truth/falsehoods
Like diagnostics, we need to consider the ratio R of true and false hypotheses that are tested:
| True | False | |
|---|---|---|
| Accept | (1-β) R/(R+1) | α /(R+1) |
| Reject | β R/(R+1) | (1-α) /(R+1) |
| sum | R/R+1 | 1/R+1 |
If R is less than one (more false than true hypotheses are tested), this inflates the False/Accept, relative to True/Accept.
Another example
Stricter thresholds
(Including Bonferroni correction.)
But: reducing α inflates β.
More complex models
Number of experiments
Multiply by a factor of c:
| True | False | |
|---|---|---|
| Accept | c (1-β)R/(R+1) | c α/(R+1) |
| Reject | c β R/(R+1) | c (1-α)/(R+1) |
| sum | cR/(R+1) | c/(R+1) |
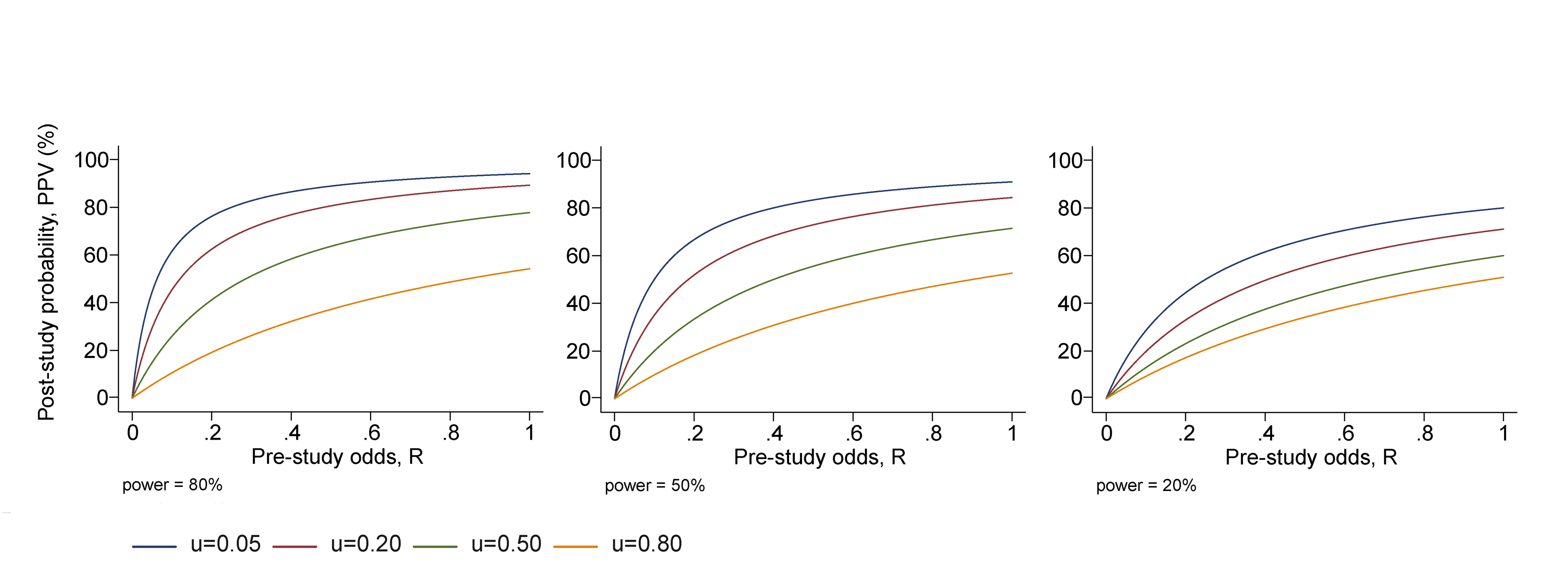
Bias
Moves a fraction, u, from Reject to Accept.
| True | False | |
|---|---|---|
| Accept | (c(1-β)R +ucβ R)/(R+1) | (cα +uc(1-α))/(R+1) |
| Reject | (1- u)cβ R/(R+1) | (1- u)c(1-α)/(R+1) |
| sum | cR/(R+1) | c/(R+1) |
Effect of bias
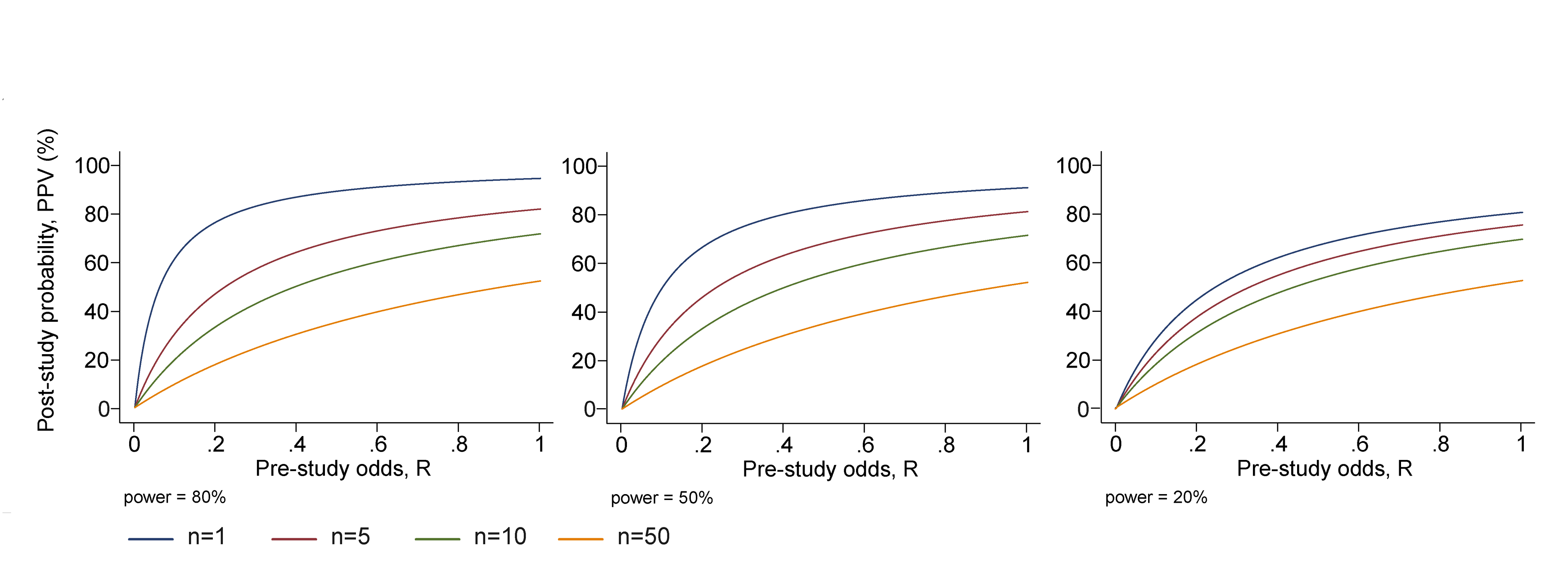
Multiple teams
Type II: β = prob of one team missing a true result
Independent teams, prob all miss it: βn
I.e. prob none miss it: 1-βn
Type I: α = prob of rejecting a false null hypothesis.
Probability that nobody rejects a false null: (1-α)n
Multiple teams
Ignoring bias, we substitute:
| True | False | |
|---|---|---|
| Accept | c(1- βn)R/(R+1) | c(1- (1-α)n)/(R+1) |
| Reject | c βn R/(R+1) | c (1-α)n /(R+1) |
| sum | cR/(R+1) | c/(R+1) |
Effect of multiple teams
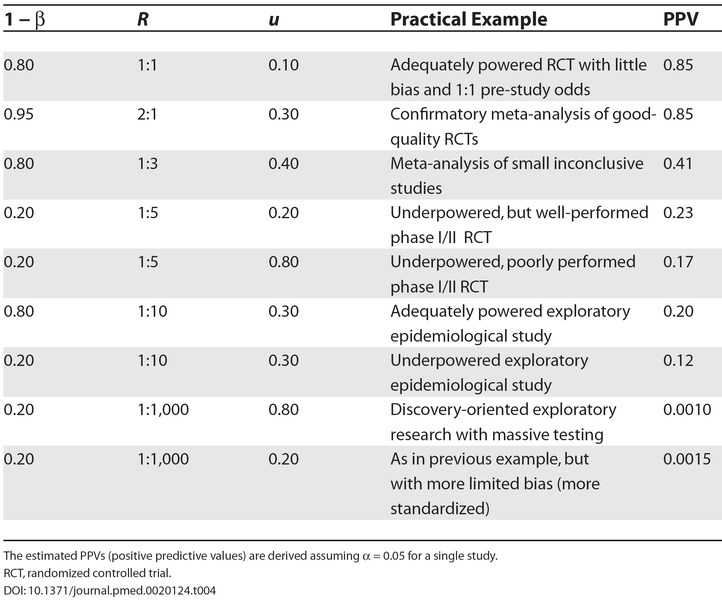
Consequences
Example cases
Small study size
The smaller the studies conducted in a scientific field, the less likely the research findings are to be true.
We knew that. How many fish can you fit in a tank?
Small effect size
The smaller the effect sizes in a scientific field, the less likely the research findings are to be true.
Reduces power. What are the typical effect sizes we look for?
Number of hypotheses tested
The greater the number and the lesser the selection of tested relationships in a scientific field, the less likely the research findings are to be true
How many genes affect a genotype? How many did we test? How common are the different variants?
Flexibility of design
The greater the flexibility in designs, definitions, outcomes, and analytical modes in a scientific field, the less likely the research findings are to be true
How do we properly analyse RNAseq data? GWAS? Epigenetics? Who wrote that program you use to predict salmon SNPs - a statistician?
Simulation suggests that false positive rates can jump to over 50% for a given dataset just by letting researchers try different statistical analyses until one works. (Simmons, et al, 2011)
Financial interest/importance
The greater the financial and other interests and prejudices in a scientific field, the less likely the research findings are to be true.
Fiskaren: Research error cost one billion.
More effort
The hotter a scientific field (with more scientific teams involved), the less likely the research findings are to be true
Empirical evidence suggests that [publishing of dramatic results, followed by rapid refutations] is very common in molecular genetics
Remedies and incentives
What can be done?
Larger studies
- Focus on likely hypotheses
- Bias still important
Formalized methods
- Preregistration of experiments
- Enforce publication of negative results
- Predetermined analysis
(I.e. no data dredging)
Scientific producitivity
Measurements of productivity:
- number of publications
- number of citations
- publications in high-ranking journals
Summa summarum
- scientists benefit from low quality science
- institutions benefit
- journals benefit
It's a win-win situation!
(Except if you care about, you know, science)
References
- Ioannides: Why most… PLoS Medicine 2005.
- Trouble at the Lab The Economist, Oct 19, 2013
- http://www.statisticsdonewrong.com